BP算法笔记

2021-11-19

定义：

BP(Back Propagation)算法是由学习过程由信号的正向传播与误差的反向传播两个过程组成。由于多层前馈网络的训练经常采用误差反向传播算法，人们也常把将多层前馈网络直接称为BP网络。

前期准备：

为了更好地了解BP算法，首先我们要对神经网络有个大致了解：

神经网络基本概述

人工神经网络包括多个神经网络层，如卷积层、全连接层、LSTM等，每一层又包括很多神经元，超过三层的非线性神经网络都可以被称为深度神经网络。通俗的讲，深度学习的模型可以视为是输入到输出的映射函数，如图像到高级语义（美女）的映射，足够深的神经网络理论上可以拟合任何复杂的函数。因此神经网络非常适合学习样本数据的内在规律和表示层次，对文字、图像和语音任务有很好的适用性。因为这几个领域的任务是人工智能的基础模块，所以深度学习被称为实现人工智能的基础也就不足为奇了。
神经元：神经网络中每个节点称为神经元，由两部分组成：
加权和：将所有输入加权求和。
非线性变换（激活函数）：加权和的结果经过一个非线性函数变换，让神经元计算具备非线性的能力。
多层连接：大量这样的节点按照不同的层次排布，形成多层的结构连接起来，即称为神经网络。
前向计算：从输入计算输出的过程，顺序从网络前至后。
后向传播：更新、优化参数
计算图：以图形化的方式展现神经网络的计算逻辑又称为计算图。我们也可以将神经网络的计算图以公式的方式表达，如下：
Y = f3(f2(f1(w1x1+w2x2+w3*x3+b)+…)…)
由此可见，神经网络并没有那么神秘，它的本质是一个含有很多参数的“大公式”
神经网络基本结构
1.类似于人大脑的结构，由“神经元”构成，可暂时理解成一个用来装数字的容器，装着0到1之间的数字，这些数字代表对应像素的灰度值，并称为“激活值”，值越大该神经元越亮。
2.神经网络有多个层，其中第一层叫“输入层”，最后一层叫“输出层”，中间的叫“隐含层”
3.上一层的激活值将决定决定下一层的激活值，某些神经元的激发，就会促使另一些神经元激发，”输出层”最亮的神经元就是输出值。
4.前一层所有的激活值乘相应权重之和再加上偏置，最后送进sigmoid函数中，才使下一层的某个神经元激发得更有意义。

BP算法基本思想：

学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时，输入样本从输入层传入，经各隐层逐层处理后，传向输出层。若输出层的实际输出与期望的输出(教师信号)不符，则转入误差的反向传播阶段。误差反传是将输出误差以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程，是周而复始地进行的。权值不断调整的过程，也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可接受的程度，或进行到预先设定的学习次数为止。

反向传播：

反向传播是神经网络学习的核心算法，可用来求梯度，以找到Loss函数的最小值。
1.权重越大证明对梯度的影响越大，要尽快找到函数的最小值，就对相应的权重进行增减，不能盲目，选择性价比高的参数。
2.要得到想要的结果，就要增加相应的激活值，有三条大路可走：一，增加偏置；二，增加权重；三，改变上一层激活值。但我们能做的是头上偏置和权重的改变。
3.我们还需要把最后一层其余神经元激发变弱，但对于如何改变倒数第二次，都有各自的想法。所有，我们会把需要的神经元的期待，和别的输出神经元的期待全部加起来，作为对如何改变倒数第二层神经元的指示，这些期待变化不仅是对应的权重的倍数，也是每个神经元激活值改变量的倍数，这就是在实现“反向传播”的理念了
4.把所有期待的改变加起来，就得到一串对倒数第二层改动的变化量，重复这个过程，一直循环到第一层。

实例：

以波士顿房价预测问题为例：

数据处理

其中包括：数据导入、数据形状变换、数据集划分、数据归一化处理和封装load data函数。

模型设计：

模型设计是深度学习模型关键要素之一，也称为网络结构设计，相当于模型的假设空间，即实现模型“前向计算”（从输入到输出）的过程。

前向传播算法：

前向计算的过程是：输入含有13个特征的数据x，输出1个预测的房价y。
$$ y=x⋅w+b $$
x为每一条数据shape：[1,13]
则权值矩阵w的shape：[13,1]
b为偏置，是一个标量
代码如下：

class Network(object):
    def __init__(self,num_of_weights):
        #s随机产生w的初始值
        #为了保持程序每次运行结果的一致性，设置固定的随机数种子
        np.random.send(0)
        self.w = np.random.randa(num_of_weights,1)
        self.b = 0
        
    def forward(self,x):
        z = np.dot(x,self.w) + self.b
        return z

损失函数设计：

用损失函数可以衡量实际房价y和通过模型输出预测房价z的差距，从而衡量模型的好坏，对于回归问题，最常采用的衡量方法是使用均方误差作为评价模型好坏的指标
$$ Loss=(y−z)^2 $$
代码演示如下：

def loss(self, z, y):
    error = z-y
    cost = error * error
    cost = np.mean(cost)  #对向量取均值操作
    return cost

梯度下降算法：

梯度计算：

模型的训练的目的是使损失函数的值不断减小，而函数值下降最快的方向是沿着梯度的反方向。
梯度的定义：
数学计算：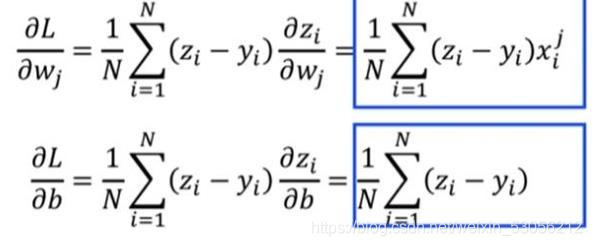

代码实现如下：

def gradient(self,x,y):
    z = self.forward(x)
    gradient_w = (z-y)*x
    gradient_w = np.mean(gradient_w,axis=0)
    gradient_w = gradient_w[:,np.newaxis]
    gradient_b = (z-y)
    gradient_b = np.mean(gradient_b)
    return gradient_w,gradient_b

梯度更新与训练：

代码实现如下：

def update(self,gradient_w,gradient_b,eta = 0,01): #定义步长eta     
    # 梯度更新
    # 沿着梯度的反方向移动到下一个点P1 
    self.w = self.w - eta * gradient_w
    self.b = self.b - eta * gradient_b
def train(self,x,y,iterations=100,eta = 0.01):
    losses = []
    for i in range(iterations):
        z = self.forward(x)
        L = self.loss(z,y)
        gradient_w,gradient_b = self.gradient(x,y)
        self.update(gradient_w,gradient_b,eta)
        losses.append(L)
        if (i+1) %10 == 0:
            print('iter{},loss{}'.format(i,L))
    return losses

不足点：

主要表现在训练过程不确定上，具体如下：

训练时间较长。对于某些特殊的问题，运行时间可能需要几个小时甚至更长，这主要是因为学习率太小所致，可以采用自适应的学习率加以改进。
完全不能训练。训练时由于权值调整过大使激活函数达到饱和，从而使网络权值的调节几乎停滞。为避免这种情况，一是选取较小的初始权值，二是采用较小的学习率。
易陷入局部极小值。BP算法可以使网络权值收敛到一个最终解，但它并不能保证所求为误差超平面的全局最优解，也可能是一个局部极小值。这主要是因为BP算法所采用的是梯度下降法，训练是从某一起始点开始沿误差函数的斜面逐渐达到误差的最小值，故不同的起始点可能导致不同的极小值产生，即得到不同的最优解。如果训练结果未达到预定精度，常常采用多层网络和较多的神经元，以使训练结果的精度进一步提高，但与此同时也增加了网络的复杂性与训练时间。
“喜新厌旧”。训练过程中，学习新样本时有遗忘旧样本的趋势。

改进：

随机梯度下降算法：

在实际问题中，数据集往往非常大，如果每次都使用全量数据进行计算，效率非常低，通俗地说就是“杀鸡焉用牛刀”。由于参数每次只沿着梯度反方向更新一点点，因此方向并不需要那么精确。一个合理的解决方案是每次从总的数据集中随机抽取出小部分数据来代表整体，基于这部分数据计算梯度和损失来更新参数，这种方法被称作随机梯度下降法（Stochastic Gradient Descent，SGD）。

代码实现如下：

import numpy as np
class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子
        #np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)
        self.b = 0.
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z
    
    def loss(self, z, y):
        error = z - y
        num_samples = error.shape[0]
        cost = error * error
        cost = np.sum(cost) / num_samples
        return cost
    
    def gradient(self, x, y):
        z = self.forward(x)
        N = x.shape[0]
        gradient_w = 1. / N * np.sum((z-y) * x, axis=0)
        gradient_w = gradient_w[:, np.newaxis]
        gradient_b = 1. / N * np.sum(z-y)
        return gradient_w, gradient_b
    
    def update(self, gradient_w, gradient_b, eta = 0.01):
        self.w = self.w - eta * gradient_w
        self.b = self.b - eta * gradient_b
            
                
    def train(self, training_data, num_epoches, batch_size=10, eta=0.01):
        n = len(training_data)
        losses = []
        for epoch_id in range(num_epoches):
            # 在每轮迭代开始之前，将训练数据的顺序随机打乱
            # 然后再按每次取batch_size条数据的方式取出
            np.random.shuffle(training_data)
            # 将训练数据进行拆分，每个mini_batch包含batch_size条的数据
            mini_batches = [training_data[k:k+batch_size] for k in range(0, n, batch_size)]
            for iter_id, mini_batch in enumerate(mini_batches):
                #print(self.w.shape)
                #print(self.b)
                x = mini_batch[:, :-1]
                y = mini_batch[:, -1:]
                a = self.forward(x)
                loss = self.loss(a, y)
                gradient_w, gradient_b = self.gradient(x, y)
                self.update(gradient_w, gradient_b, eta)
                losses.append(loss)
                print('Epoch {:3d} / iter {:3d}, loss = {:.4f}'.
                                 format(epoch_id, iter_id, loss))
        
        return losses

总结：

实现逻辑：

前向计算输出
根据输出和真实值计算Loss
基于Loss和输入计算梯度
根据梯度更新参数值
前四个部分反复执行，直到到达参数最优点